"IL MONDO COME IO LO VEDO"

«Il mondo come io lo vedo»

     ''Due cose sono
       infinite: l'universo 

       e la stupidità umana

       E non sono così sicuro 

       per quanto riguarda 

       l'universo.''

       Albert Einstein

La crisi secondo Einstein

“Non possiamo pretendere che le cose cambino, se continuiamo a fare le stesse cose. La crisi è la più grande benedizione per le persone e le nazioni, perché la crisi porta progressi. La creatività nasce dall’angoscia come il giorno nasce dalla notte oscura. E’ nella crisi che sorge l’inventiva, le scoperte e le grandi strategie. Chi supera la crisi supera sé stesso senza essere ‘superato’. Chi attribuisce alla crisi i suoi fallimenti e difficoltà, violenta il suo stesso talento e dà più valore ai problemi che alle soluzioni. La vera crisi, è la crisi dell’incompetenza. L’inconveniente delle persone e delle nazioni è la pigrizia nel cercare soluzioni e vie di uscita. Senza crisi non ci sono sfide, senza sfide la vita è una routine, una lenta agonia. Senza crisi non c’è merito. E’ nella crisi che emerge il meglio di ognuno, perché senza crisi tutti i venti sono solo lievi brezze. Parlare di crisi significa incrementarla, e tacere nella crisi è esaltare il conformismo. Invece, lavoriamo duro. Finiamola una volta per tutte con l’unica crisi pericolosa, che è la tragedia di non voler lottare per superarla”.

(da Il mondo come io lo vedo di Albert Eistein)

Matematica Dilettevole e Curiosa

      ***Matematica Dilettevole e Curiosa***

UN FURBO E UN AVARO

Un mendicante domanda ospitalità ad un avaro che non vuole accordargliela gratuitamente.

Il mendicante gli fa allora questa proposta:

Vi pagherò, dice, 1 lira per il primo giorno, 2 lire il secondo giorno, 3 lire il terzo, 4 lire il quarto e così di seguito. Voi invece mi darete un millesimo di centesimo il primo giorno, due millesimi di centesimo il secondo giorno, quattro millesimi di centesimo il terzo giorno, otto millesimi di centesimo il quarto giorno e così' di seguito.

L'avaro trovò la proposta originale e la giudicò conveniente, ma volle limitare l' ospitalità a 30 giorni tanto per non avere sorprese.

Chi ci guadagno?

 Risposta:

Evidentemente l'avaro, colpito dal suono delle cifre, assolutamente conveniente del mendicante, accettò la proposta sia pure per 30 giorni senza sapere quale mazzata gli arrivava in testa alla fine dei 30 giorni per effetto del risultato che gravava sulla sua borsa in conseguenza di una progressione geometrica, mentre il debito del mendicante, proveniente da una progressione aritmetica, era irrisorio.

La somma che il mendicante pagò all'avaro fu:
S1 = a1+a2+a3+a4+...............a30;

S1=1£+2£+3£+.................30£=       
con    
dove la ragione d=1 ed n=30 è il numero di termini della progressione aritmetica con a1=1 e a30=30 mentre la somma che l'avaro pagò al mendicante fu S2 = a1+a2+a3+.............+a30   =



somma dei primi 30 termini di una progressione geometrica

 dove la ragione q=2  e          

                                GLI ELEMENTI DI EUCLIDE

Gli ELEMENTI, un trattato che, per numero di edizioni e di traduzioni può competere con La Divina Commedia dantesca e, forse, è superato solo dalla Bibbia.

L'opera di Euclide rappresenta una sintesi organica delle conoscenze matematiche dei suoi tempi ed è ispirata a fini didattici: per molti anni è stato usato come testo nelle scuole, con ottimi risultati.

Il miglior testo euclideo è tuttora quello curato dal filosofo e matematico olandese J.L. Heiberg che fu uno dei più profondi conoscitori della matematica e della letteratura greca: è in greco con testo a fronte in latino. In italiano è da menzionare l'edizione curata da F. Enriques  e dai suoi collaboratori, che hanno tradotto l'intera opera euclidea.

Gli ELEMENTI si compongono di 13 libri, nei quali si trova esposta sistematicamente tutta la geometria elementare. Ogni libro inizia con un gruppo di proposizioni che possono essere considerate come una specie di definizioni che servono a chiarire i concetti successivi; esse sono seguite da altre proposizioni che sono invece veri e propri problemi o teoremi: questi si differenziano fra di loro per il modo con cui vengono enunciati e la frese rituale con cui si chiudono: "come dovevasi fare" per i problemi, "come dovevasi dimostrare" per i teoremi. I principi fondamentali esposti negli Elementi si distinguono in tre categorie: termini o definizioni, postulati (di natura geometrica) e nozioni comuni(postulati anch'essi, ma di portata più generale).

I tredici libri dell'opera  trattano:

1. Il Libro I la teoria dei triangoli, delle parallele e delle aree (ciò che oggi chiamiamo equivalenza di figure piane);
2. Il Libro II la cosiddetta algebra geometrica
3. Il Libro III la teoria del cerchio
4. Il Libro IV le proprietà e le costruzioni dei poligoni inscritti e circoscritti
5. Il Libro V la teoria dei rapporti tra grandezze e delle proporzioni astratte
6. Il Libro VI la teoria della similitudine e delle proporzioni in geometria
7. Il Libro VII la teoria fondamentale dei numeri
8. Il Libro VIII le proporzioni continue nella teoria dei numeri
9. Il Libro IX ancora la teoria dei numeri
10. Il Libro X la teoria degli incommensurabili
11. Il Libro XI la geometria solida
12. Il Libro XII la misura delle figure solide
13. Il Libro XIII i solidi regolari

LA BOTTEGA DEL MATEMATICO

Un prototipo di situazione didattica efficace

.........l’insegnamento della matematica nelle scuole superiori presenta ancora oggi molti difetti. 

1. Spesso l’insegnante sviluppa prima la teoria,dando definizioni, enunciando e dimostrando teoremi, e poi la applica o la fa applicare agli allievi nella risoluzione di esercizi spesso ripetitivi, o di problemi che anche se complessi “si sa già come trattare”. Spesso gli esercizi e i problemi affrontati a scuola hanno come risultato quello di consolidare forme di automatismi piuttosto che quello di indurre i ragazzi al ragionamento. 
2. Spesso l’insegnante è convinto che si debbano subito portare gli studenti verso la formalizzazione e dimentica l’importanza di far riferimento a situazioni concrete. Ne deriva che gli studenti sono spesso incapaci di utilizzare la matematica come strumento per descrivere e rappresentare la realtà.
3. Spesso l’insegnante mira solo alla disciplina “matematica”, quella che si trova bene ordinata nei libri di scuola, svuotandola perciò del suo significato e rendendola, il più delle volte, arida agli occhi degli studenti.
4. Spesso l’insegnante favorisce negli allievi la suddivisione delle conoscenze matematiche in settori separati tra loro. Rare sono le occasioni in cui li spinge ad usare tutta quanta la matematica e non solo una piccola parte. Ai ragazzi viene così a mancare un quadro complessivo del sapere matematico e delle relazioni fondamentali esistenti tra le diverse aree.
5. Spesso l’insegnante favorisce negli allievi la suddivisione delle conoscenze matematiche in settori separati tra loro. Rare sono le occasioni in cui li spinge ad usare tutta quanta la matematica e non solo una piccola parte. Ai ragazzi viene così a mancare un quadro complessivo del sapere matematico e delle relazioni fondamentali esistenti tra le diverse aree.

Come si possono superare tali limiti? Nella Bottega del Matematico i docenti  partono da situazioni problematiche. Invece di iniziare la trattazione di un argomento con una serie di definizioni e teoremi, i docenti lanciano dei problemi la cui risoluzione porta alla scoperta di un nuovo concetto o allo sviluppo di una teoria. Può essere efficace anche a scuola una tale scelta metodologica? Vediamo di esaminare i punti di forza di una didattica di questo tipo:

1. può suscitare l’interesse e la partecipazione di tutti gli allievi;
2. coinvolge gli studenti e scatena la loro fantasia nel creare ipotesi per cui essi divengono veramente attivi e si calano nello“spirito del ricercatore” per risolvere i problemi;
3. li porta a costruire nuovi concetti e abilità e nello stesso tempo a consolidare quelli acquisiti in precedenza;
4. li spinge ad avere il coraggio di sbagliare,di riconoscere i propri errori e di costruire ipotesi sempre più valide;
5. li avvicina sempre di più al modo di lavorare del ricercatore, il quale, una volta che ha inciampato in un problema, procede per tentativi ed errori verso la ricerca della soluzione;
6. li motiva intrinsecamente all’ apprendimento della matematica;
7. combatte il nozionismo: un problema trasforma una nozione qualsiasi in una nozione importante, rilevante per quel problema.

Qualcuno si potrebbe però domandare se non vi siano altre strategie ugualmente efficaci per ottenere gli stessi risultati. Se pensiamo però al modo di procedere della scienza, ci accorgiamo che la ricerca scientifica parte sempre da problemi e che lo scienziato si trova il più delle volte ad inciampare in problemi, che rappresentano per lui situazioni nuove, per le quali non ha pronte delle soluzioni. Lo stesso sapere matematico «nasce da un’attività comune su problemi significativi, di cui si parla e si discute». Queste considerazioni inducono quindi a pensare che il modo più autentico di fare matematica sia quello di risolvere problemi e che le conoscenze e le abilità matematiche si possano imparare «lavorando attivamente in situazioni significative, discorrendo di quello che si fa, calandosi in contesti specifici, passando da un contesto all’altro e producendo infine concetti decontestualizzati, pronti ad essere usati in nuovi contesti».

*****Matematica Dilettevole e Curiosa*****

LE FATICHE DEL FACCHINO

Un facchino deve distribuire 6 oggetti a 6 inquilini d'una casa che abitano a ciascuno dei 6 piani. Egli non può portare che un oggetto alla volta. Tra un piano e l'altro vi è una scala di 21 gradini e tra la strada e il piano del portico vi sono altri 7 gradini. Quanti gradini dovrà in tutto salire quel facchino per portare tutti gli oggetti a destinazione?

Soluzione

Per portare il primo oggetto il facchino sale 7 gradini, per il secondo 7+21,  per il terzo 7+21+21 etc.

Egli sale in totale un numero di gradini dato dalla somma  dei termini di una progressione aritmetica di 6 termini dei quali il primo è 7 e l'ultimo 7+5*21 e la ragione 21 ossia:

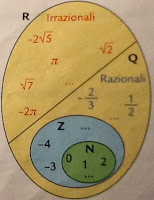
LA MATEMATICA DEL SUPERENALOTTO ( calcolo delle probabilità!)

Azzeccare un 6 al Superenalotto è difficilissimo: molto più difficile che essere colpiti da un asteroide.

                                                         Fig.1

1. Il concetto di probabilità: un concetto matematico molto semplice.

E’ un concetto che in realtà quasi tutti abbiamo in testa. Ma cerchiamo di dargli una sistemazione un po’ più formale. Quando lanciamo un dado a sei facce, qual è la probabilità che esca il numero 3? Ovviamente è un sesto: 6 sono i numeri che possono uscire, uno solo è quello che vogliamo che esca (il numero 3). Ecco, una delle definizioni matematiche della probabilità è proprio il rapporto fra il numero degli eventi favorevoli e il numero degli eventi possibili. Nel nostro esempio precedente, l’unico evento favorevole (cioè, quello di cui stiamo calcolando la probabilità che accada) è il fatto che esca il numero 3, mentre gli eventi possibili sono tutti i sei numeri che possono uscire (1,2,3,4,5,6).

Teniamo ora a mente la definizione della probabilità matematica:


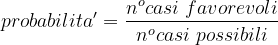
Torniamo al SuperEnalotto. Supponiamo di aver giocato una sestina particolare, come per esempio,

1 2 3 4 5 6

allora l’evento favorevole è che  esca proprio la sestina 1 2 3 4 5 6, e quindi abbiamo solo un evento favorevole. Quanti sono gli eventi possibili? Cioè, quante sono le sestine possibili che possono esere estratte? Per dare una risposta alla precedente domanda, facciamo il seguente ragionamento:

2. Contare le sestine (combinazioni semplici): per vincere bisogna saper contare!

Prendiamo il caso più semplice dei dadi. Se lanciamo due dadi (Fig.1), quante sono le coppie ordinate (contate con ordine) che possono uscire? Al lancio del primo dado possono uscire 6 numeri diversi, e lo stesso vale per il secondo dado, e quindi abbiamo 6⋅6=36 coppie ordinate possibili.

Adesso facciamo lo stesso ragionamento sulle sestine. Alla prima estrazione può uscire un qualunque numero fra i 90 presenti nell’urna, e quindi abbiamo 90 possibilità. Alla seconda estrazione, invece, siccome abbiamo già tolto un numero, avremo solo 89 possibilità, e così via alla terza avremo 88 possibilità, alla quarta 87 possibilità, alla quinta 86 possibilità e alla sesta estrazione 85 possibilità. In tutto abbiamo quindi 90⋅89 ⋅88 ⋅87 ⋅86 ⋅85= 448282533600 sestine possibili.

Attenzione! Abbiamo contato delle sestine in più! Nelle estrazioni non conta l’ordine in cui i numeri vengono estratti! Per esempio, estrarre in ordine i numeri 2 3 4 5 6 7 equivale all’estrazione degli stessi numeri ma in un altro ordine, per esempio 7 3 2 4 5 6 (si vince in entrambi i casi!). Allora con il numero 448282533600 abbiamo contato non solo tutte le sestine possibili ma tutte le sestine possibili ordinate in tutti i modi possibili (e già, in matematica l’ordine conta)! Per sapere solo il numero delle sestine possibili bisogna dividere per un numero che corrisponde al numero di modi possibili di ordinare una sestina di numeri perché abbiamo contato ogni sestina più di una volta!

E allora in quanti modi posso ordinare una sestina di numeri? Facciamo un ragionamento matematico simile a prima. Il primo numero può essere scelto in 6 modi, il secondo in 5 perché un numero è già stato scelto, il terzo in 4, il quarto in 3, il quinto in 2 e il sesto numero può essere scelto in un solo modo (quello che è rimasto). Quindi, dati sei numeri, abbiamo 6⋅5 ⋅4 ⋅3 ⋅2 ⋅1 modi di ordinarli.

3. Conclusione: vincere? E’ molto raro e te lo dice la Matematica!

In conclusione, il numero totale delle sestine, senza contare l’ordine, che possono essere estratte  sono

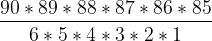
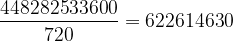
          e cioè                           

   
Ricapitolando, abbiamo calcolato:

• il numero di eventi favorevoli = 1               (la sestina che abbiamo scelto prima dell’estrazione)
• il numero di eventi possibili = 622614630  (tutte le sestine che possono uscire in una estrazione)

Ricordando la formula della probabilità:



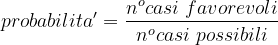
Abbiamo che la probabilità di vincere una sestina al SuperEnalotto è  

che in percentuali è circa 0.00000016 %

Adesso capite quanto è difficile vincere al SuperEnalotto!

NUMERI ALGEBRICI E TRASCENDENTI

Considerando gli insiemi numerici, possiamo pensare ai numeri reali R come l'unione dell'insieme dei numeri razionali Q e l'insieme dei numeri irrazionali I.

Fig.1

Sappiamo inoltre che   (Fig.1)

Esiste anche un'altra classificazione che divide i numeri reali R in numeri algebrici e numeri trascendenti:

1. Un numero si dice algebrico se è soluzione di una equazione polinomiale a coefficienti razionali;
2. Un numero si dice trascendente se NON è soluzione di una equazione polinomiale a coefficienti razionali;

Esempio:

1. 5 è un numero algebrico perchè soluzione dell'equazione a coefficienti razionali x-5=0;
2.  è un numero algebrico perchè soluzione dell'equazione a coefficienti razionali ;
3.  è un numero trascendente perchè non è soluzione di nessuna equazione polinomiale a coefficienti razionali.

N.B. I numeri razionali Q sono tutti algebrici;

        I numeri irrazionali I possono essere sia algebrici che trascendenti.

LA QUADRATURA DEL CERCHIO

LA QUADRATURA DEL CERCHIO

Nell'antica Grecia era molto popolare il problema della quadratura del cerchio: come costruire con riga e compasso il quadrato con area uguale a un cerchio. Questo è un problema molto più complicato del problema delle tre giare. Anzi, adesso sappiamo bene che non ha soluzione. I greci di quel tempo, però, ci perdevano il sonno: era tanto popolare che il commediografo Aristofane lo citò nella sua opera "Gli uccelli". Non solo: per indicare una persona "impegnata a fare altro" i greci avevano addirittura coniato un'espressione particolare, che equivaleva all'essere "occupati alla risoluzione della quadratura". e da questo si può capire che il problema non era riservato ai soli matematici, ma anzi era ampiamente condiviso da tutti. Tra i vari tentativi di soluzione, il "più esatto" è il metodo proposto dall'oratore Antifonte. nel V secolo a.C.: in pratica, suggeriva di eguagliare l'area del cerchio inscrivendo poligoni regolari con molti lati. Una soluzione richiede la costruzione del numero sqrt{π}, e l'impossibilità di ciò deriva dal fatto che π è un numero trascendente, ovvero non-algebrico, e quindi non-costruibile. La trascendenza di π venne dimostrata da Ferdinand von Lindemann nel 1882. Risolvere il problema della quadratura del cerchio, significa aver trovato anche un valore algebrico di π - il che è impossibile. Ciò non implica che sia impossibile costruire un quadrato con un'area molto vicina a quella del cerchio dato. Altri particolari problemi affrontati dai matematici greci sono quelli della trisezione di un angolo e della duplicazione del cubo. anch'essi non sono risolvibili col solo uso di riga e compasso, ma per il secondo, quello di riuscire a costruire un cubo con volume doppio di un cubo dato, sono state trovate varie soluzioni tridimensionali. ad esempio Archita di Taranto (430-460 a.C.) trovò una soluzione intersecando un cilindro, un cono e il cosiddetto "toro" (la superficie di una ciambella).

L'OFFICINA MATEMATICA

L'OFFICINA MATEMATICA DI
EMMA CASTELNUOVO

..........il suo insegnamento si fonda su un metodo non direttivo (che infonde le conoscenze dall'insegnante all'allievo), che si esprime facendo costruire le conoscenze ai ragazzi stessi, i veri protagonisti della situazione. Imparare vuol dire costruire il proprio sapere e in questo senso, il metodo di Emma Castelnuovo, si pone a fondamento di qualsiasi situazione di apprendimento che vede impegnato l'alunno in una vera e propria opera di costruzione delle conoscenze insieme agli altri. La didattica di Emma è attiva e non avviene facendo stare seduti gli alunni al proprio banco "in attesa che possano essere illuminati": stimola nei ragazzi l'amore alla ricerca, il gusto di apprendere, di mettersi alla prova per sperimentare le proprie attitudini e l'intelligenza logico-matematica.

I pilastri innovativi della didattica di Emma sono:
1. Guidare l'alunno alla riscoperta delle leggi e proprietà dei numeri e delle figure
2. Considerare le problematiche concrete come base di ricerca, capaci di coinvolgere l'alunno
3. Utilizzare un indirizzo storico-costruttivo e non descrittivo.

Emma Castelnuovo suggerisce:

1) ....una didattica che sappia rispettare i tempi dell'alunno e il suo modo di mettersi alla prova "cimentandosi" per sviluppare le possibilità di osservazione, l'intuizione, il senso critico, e, in generale, alcune fondamentali attitudini di pensiero.

2) "......mettersi allo stesso livello, cioè suscitare interesse e quindi discussioni, accettare domande su domande, anche le più balorde! Accettare delle domande a cui, là per là, non si sa rispondere e non avere scrupolo di dire: guardate non lo so. Questa è la cosa fondamentale indipendentemente dalla materia che si insegna".

3) "Lasciate ai ragazzi il tempo di perdere tempo", nel senso di garantire loro l'opportunità di costruire soluzioni, anzichè far loro usare soluzioni già pronte. il che è come dire dare loro il tempo per riflettere, per pensare, per ipotizzare, per operare con la mente, per arrivare a capire e, quindi, a costruire conoscenze sicure.

4)" Se ci si dà il tempo necessario a che ciascuno capisca, se si condivide l'esperienza in uno spazio adatto e c'è un clima cooperativo capace di accogliere i pensieri,  le ipotesi e le idee di ciascuno, alcuni ostacoli e blocchi mentali possono essere attenuati e tutti hanno la possibilità di esprimersi senza paura di sbagliare".

Nobel  Enrico Fermi (1901-1954)

LA DIDATTICA DI FERMI.........

Racconto di Yang sulla didattica di Fermi

                     "Se l’uomo non sapesse di 
             matematica non si eleverebbe di un 
             sol palmo da terra"

                                                                  Galileo Galilei

  "E' meglio una testa ben fatta che una testa ben piena"

                                                                   (Michel de Montaigne)

        "… la mente non ha bisogno, come un vaso, di essere riempita, ma,
    come legna da ardere, ha bisogno solo di una scintilla che la accenda,

                     che vi infonda l'impulso alla ricerca e il desiderio della verità"

                                                              (Plutarco, Moralia, De audiendo)