LA QUADRATURA DEL CERCHIO

Un Cerchio e un Quadrato con aree equivalenti

Qual è ‘l geomètra che tutto s’affige

            per misurar lo cerchio, e non ritrova, 

            pensando, quel principio ond’ elli indige, 

            tal era io a quella vista nova: 

            veder voleva come si convenne

            l’imago al cerchio e come vi s’indova; 

            ma non eran da ciò le proprie penne: 

  (Dante, Divina Commedia, Paradiso, Canto XXXIII, vv 133-139)

Se vogliamo costruire il quadrato di area equivalente al cerchio dobbiamo costruire un quadrato di lato . Il problema della quadratura del cerchio trae origine dal concetto greco di costruibilità. Nell'antica Grecia gli strumenti ammessi  per le costruzioni geometriche erano riga e compasso, tutto questo porta ad ottenere una categoria di numeri noti come numeri costruibili. Ricordiamo che ogni numero costruibile è algebrico pur sapendo che l'insieme dei numeri algebrici comprende sia i numeri costruibili che i numeri non costruibili: un numero è algebrico quando è soluzione di una equazione a coefficienti razionali.

I numeri che non sono algebrici si chiamano trascendenti( formano un insieme infinito non numerabile, non contabile).

Lindemann dimostrò nel 1882 che 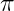 è trascendente,  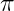pertanto non è algebrico e costruibile e pertanto non si può costruire con riga e compasso come etc. Lindemann(1852-1939) dimostrò che il problema della quadratura del cerchio è pertanto impossibile!

Reali

Diagramma di Venn che mostra la relazione tra numeri costruibili, gli algebrici, i trascendenti e i reali

=Numeri Trascendenti;    C= Numeri Costruibili

Ricordiamo:

Un numero reale a è costruibile con riga e compasso se lo è un segmento di lunghezza pari a |a| (avendo fissato un segmento di lunghezza unitaria).

I numeri interi sono costruibili con riga e compasso. Fissiamo un segmento U come unità di misura. A partire da U possiamo costruire un qualsiasi numero naturale n (basta riportare il segmento n volte su una retta) e quindi un qualunque numero intero. 

I numeri razionali sono costruibili con riga e compasso basta riportare su una retta a partire da un punto O m volte il segmento U ed dividere il segmento ottenuto in n parti uguali applicando il teorema di Talete.

Sono inoltre costruibili: 
 -la somma e la differenza di due numeri costruibili a e b 

 - il prodotto di due numeri a·b 

 - il quoziente di due numeri a/b 

 - la radice di un numero costruibile