IPERSPAZIO

Quando parliamo di iperspazio facciamo riferimento allo spazio a "n" dimensioni. Dal punto di vista matematico possiamo immaginare che se sul piano (2 dimensioni) un punto è individuato da una coppia di coordinate (x; y) e nello spazio (3 dimensioni) da una terna di coordinate (x; y ; z)  in uno spazio a "n" dimensioni  il punto sarà individuato da una ennupla  di coordinate. Anche le equazioni di rette, piani e curve si possono ricavare seguendo il segunte ragionamento: se una retta nel piano ha equazione ax + by + c = 0 e un piano nello spazio ax + by + cz + d = 0 allo stesso modo in uno spazio a "n" dimensioni una varietà a n-1 dimensioni avrà equazione 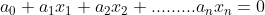. E se l'equazione di una circonferenza nel piano è 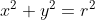 e quella della sfera nello spazio è 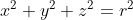 allora una ipersfera in uno spazio a n dimensioni avrà equazione .

fig.1

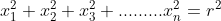In fig.1 si può seguire il passaggio dalla dimensione 1 alla dimensione 4 aggiungendo ogni volta un punto alla figura precedente fino ad arrivare alla costruzione dell'ipertetraedro.
Sappiamo che il concetto di spazio a 4 dimensioni trova applicazione nella teoria di Einstein della relatività generale(1916) tanto che il fenomeno fisico campo gravitazionale viene interpretato come curvatura dello spazio tempo a 4 dimensioni. Per formulare la  teoria della relatività generale Einstein si appoggiò al lavoro della scuola di geometria italiana, in particolare al calcolo tensoriale sviluppato da Levi-Civita e Ricci-Curbastro. Alla teoria dello spazio a 4 dimensioni seguirono teorie per spazi a  5 dimensioni per giustificare anche il campo elettromagnetico, e di recente sono state proposte teorie con un numero maggiore di dimensioni nel tentativo di giustificare tutte le interazioni fisiche come è il caso della teoria delle stringhe.

Coordinate oblique e polari di uno
spazio euclideo bidimensionale

                           

Spazio ad una dimensione

Prospettiva come rappresentazione
 bidimensionale di uno spazio tridimensionale

Spazio tridimensionale