 |
| Leibniz - Newton e...il calcolo infinitesimale |
Nella geometria, nella fisica, ed in generale nelle applicazioni della matematica allo studio dei fenomeni naturali, ed anche sociali si presentano problemi quali: calcolo delle aree, di lunghezze, di volumi, di centri di gravità, di momenti di inerzia, di lavori etc. per la risoluzione dei quali è necessario ricorrere al calcolo integrale.
Le prime origini del calcolo integrale risalgono ai geometri greci come: Eudosso di Cnido, Archimede, etc...)solo però nel XVII secolo la teoria raggiunge un livello tale che in tale periodo viene data una rigorosa definizione di integrale definito di una y=f(x) continua .
1) Tabella derivate fondamentali e regole di derivazione2) Lezione Derivata
3) Esercizi derivate
4*)Le origini del concetto di derivata (23/10/13)
 |
| Integrali Indefiniti |
4) Appunti Integrali Indefiniti
10) Esercizi sul metodo di integrazione per parti11) Metodo di integrazione per parti
12) Video metodo di integrazione per decomposizione
13) Esercizi integrali indefiniti
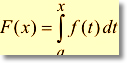 |
| F(x)=Funzione Integrale(primitiva) con F'(x)=f(x) |
15) Esercizi integrali definiti (aree e volumi)
17) Video integrazione funzioni razionali fratte (1)
18) Teoria integrali indefiniti
19) Video risoluzione integrale con delta<0
 |
| f(c)= Valore Medio di f(x) in [a; b] |
21) Video integrazione per parti(10/10/13)
22) Capire I Vari Metodi di Integrazione (11/10/13)
23) Integrali F(x) razionali fratte (27/11/13)
 |
| Calcolo Integrale Definito |
TEOREMI
1) Funzione integrale-Teorema di Torricelli Barrow 2) Teorema della Media
3) Calcolo integrale definito
4) Mappa concettuale integrali definiti (23/10/13)
 |
| Tabella Integrali Indefiniti |

Plurirettangoli per il calcolo approssimato del trapezoide
L'integrale definito come limite di una successione convergente di plurirettangoli inscritti e circoscritti al trapezoide rappresentato da un numero indicato con il nuovo simbolo
ESERCIZI
2) Esempi terza prova E.S. integrali definiti (22/10/13)
3) Calcolo area superficie, volume solidi, lunghezza arco (29/10/13)4) Calcolo area metodo dei rettangoli (29/10/13)
5) Integrali definiti: (superficie, volumi, lunghezza curva) (30/10/13)
6) Integrale definito-teoria- (30/10/13)
INTEGRALI IMPROPRI
1) Integrali Impropri di 1^ e 2^ specie (12/11/(13)
2) Esercizi svolti per Esame di Stato (18/11/13)
3) Teoria Integrali Impropri (19/11/13)
4)Esercizi Svolti Integrali Impropri (20/11/13)
5) Formule (13/12/13)
6) Tabella Integrali (13/12/13)
MAPPE CONCETTUALI
1)Mappa Integrali 1 (6/12/13)
2)Mappa Integrali 2 (6/12/13)
3) Mappa Derivate (6/12/13)
4)Mappa Equazioni Differenziali (6/12/13)
EQUAZIONI DIFFERENZIALI
1)Equazioni Differenziali 1
 2)ABC Equazioni Differenziali
2)ABC Equazioni Differenziali3)Equazioni Differenziali 2
4) Video E.D. a Variabili Separabili 1
5)Video E.D. a Variabili Separabili 2
6)Equazioni Differenziali 3
7)Equazione Diff. a Variabili Separabili
8)Applicazione delle Equazioni Differenziali
9)Teoria Equazioni Differenziali 10/01/14
10) Videolezione equazioni differenziali (17/01/14)
11) Video Equazione Differenziale Lineare(21/01/14)
12)Equazioni_Funzionali(28/01/14)
***)ANALISI (Approccio Intuitivo)(21/01/14)
***)FORMULARIO1_MATEMATICA(24/01/14)
FORMULARIO2_MATEMATICA
ESERCIZI INTEGRALI
1)Esercizi Integrali 1
2)Esercizi Integrali 2
 |
| Tabella principali sostituzioni(integrazione per sostituzione) |
 |
| Integrazione funzioni fratte (N/D) con grado di N<grado di D |
Formulario_Derivate(30/01/14)
Analisi (30/01/14)
Equazioni_Differenziali(30/01/14)
Integrali(30/01/14)
 Le date degli esami di maturità 2014
Le date degli esami di maturità 2014
Si comincera' mercoledì 18 giugno con la prima prova per seguire poi il 19 con il secondo scritto e lunedì 23 con il quizzone della terza prova:
GIOVEDI' 19: secondo scritto
LUNEDI' 23: quiz terza prova
Dal 2014 l'estate dei maturandi sarà più spensierata: i test di accesso per le facoltà a numero chiuso non si svolgeranno più a luglio o settembre bensì ad aprile.
1)Punteggio_Credito_e_Prove_Esame_di_Stato

Stabilito ciò, possiamo andare a definire le derivate parziali.
Si dice derivata parziale della funzione f(x; y) nel punto P(x₀; y₀) rispetto alla variabile x il limite, se esiste ed è finito, del rapporto incrementale parziale rispetto a x al tendere a 0 dell'incremento ∆x:
.jpg)
* f'x(x₀; y₀);
* Dfx(x₀; y₀).
.jpg)
La sua derivata parziale rispetto a y sarà invece:
.jpg)
La sua derivata parziale rispetto a y sarà:
.jpg)
.jpg)
.jpg)


A)DEFINIZIONE DI FUNZIONE DI DUE VARIABILI
(x1,x2..xn) ---> Z=f(x1,x2...xn)
B)DOMINIO e CODOMINIO DI UNA FUNZIONE A DUE VARIABILI
1)Punteggio_Credito_e_Prove_Esame_di_Stato

*************************************
°)Requisiti Minimi (esercizi 11/02/14)
Funzioni a Due Variabili (11/02/14)
Appunti_Matematica_5IA(11/02/14)
Definizione_integrale_Indefinito
Integrali indefiniti e metodi di integrazione
Derivate e Metodi
Slides_ Integrali_ Definiti (1) (21/02/14)
Slides_Integrali_Definiti (2) (21/02/14)
Principali Teoremi Quinto Anno
Equazioni_Differenziali
**)Video equazioni Differenziali (25/02/14)
Equazioni Differenziali(esercizi) (25/02/14)
Equazioni Differenziali
Funzioni z=f(x,y)
Esercizi Svolti Equazioni Differenziali (25/02/14)
Video Teorema della Media (26/02/14)
Video Integrazione per parti (28/02/14)
Video Calcolo Area (3/03/14)
Video Primo Teorema calcolo Integrale (3/03/14)
Video esercizi risolti integrali (4/03/14)
Serie Numerica (5/03/04)
Serie_Nemerica_Sintesi(5/03/04)
Serie di Funzioni e di Potenze(5/03/04)
Serie di Fourier(5/03/04)
Equazioni_differenziali(5/03/04)
Esercizi sugli integrali (22/03/14)
Esercizi_serie_Numeriche(22/03/14)
Funzioni due variabili (01/04/14)
Funzioni_due_Variabili
Integrali _Definiti (14/04/14)
Video_Serie Notevoli (15/04/14)
SERIE TELESCOPICHE
La serie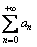 si defisce Telescopica se il termine generale an si può esprimere come differenza tra due successivi termini bn.
si defisce Telescopica se il termine generale an si può esprimere come differenza tra due successivi termini bn.
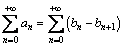 oppure
oppure 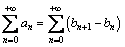
Esempio: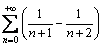
La seri di Mengoli è una serie telescopica: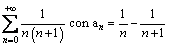 con
con
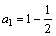
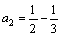
...........
sappiamo che la serie di Mengoli è convergente con somma S=1.
Video_Terza _Prova_1 (8/04/14)
°°) Video correzione verifica A (11/04/14)
Video correzione verifica B (11/04/14)
°°) I PARADOSSI DI ZENONE E LE SERIE
Paradossi di Zenone
°°)Programma svolto Matematica (24/04/14)
°°)Video esercizi Terza Prova(30/04/14)
Video Teoria Derivate Parziali (02/05/14)
Video dominio di Z=f(x,y)(02/05/14)
Punti Stazionari_ Hessiano (02/05/14)
Sintesi_Serie_Numeriche (02/05/14)
Equazioni_Differenziali (02/05/14)
Sintesi_Integrali(02/05/14)
Sintesi teoria integrali definiti e indefiniti(02/05/14)
Integrazione argomenti programma (6/05/14)

LE DERIVATE PARZIALI
Funzioni a Due Variabili (11/02/14)
Appunti_Matematica_5IA(11/02/14)
Definizione_integrale_Indefinito
Integrali indefiniti e metodi di integrazione
Derivate e Metodi
Slides_ Integrali_ Definiti (1) (21/02/14)
Slides_Integrali_Definiti (2) (21/02/14)
Principali Teoremi Quinto Anno
Equazioni_Differenziali
Equazioni Differenziali(esercizi) (25/02/14)
Equazioni Differenziali
Funzioni z=f(x,y)
Esercizi Svolti Equazioni Differenziali (25/02/14)
Video Teorema della Media (26/02/14)
Video Integrazione per parti (28/02/14)
Video Calcolo Area (3/03/14)
Video Primo Teorema calcolo Integrale (3/03/14)
Video esercizi risolti integrali (4/03/14)
Serie Numerica (5/03/04)
Serie_Nemerica_Sintesi(5/03/04)
Serie di Funzioni e di Potenze(5/03/04)
Serie di Fourier(5/03/04)
Equazioni_differenziali(5/03/04)
Esercizi sugli integrali (22/03/14)
Esercizi_serie_Numeriche(22/03/14)
Funzioni due variabili (01/04/14)
Funzioni_due_Variabili
Integrali _Definiti (14/04/14)
 |
| Grafico Serie Geom q=1/2 |
 |
| Serie Geometrica |
 |
| q=1,03 |
 |
| q=1 |
SERIE TELESCOPICHE
La serie
Esempio:
La seri di Mengoli è una serie telescopica:
...........
sappiamo che la serie di Mengoli è convergente con somma S=1.
°°)SOLUZIONI TERZE PROVE
Testo Simulazione 3° Prova Video_Terza _Prova_1 (8/04/14)
°°) Video correzione verifica A (11/04/14)
Video correzione verifica B (11/04/14)
 |
| Serie:Criterio Radice |
 |
| Serie:Criterio Rapporto |
 |
| Grafico Serie Armonica |
 |
| Grafico Serie di Mengoli |
°°) I PARADOSSI DI ZENONE E LE SERIE
Paradossi di Zenone
°°)Programma svolto Matematica (24/04/14)
°°)Video esercizi Terza Prova(30/04/14)
Video Teoria Derivate Parziali (02/05/14)
Video dominio di Z=f(x,y)(02/05/14)
Punti Stazionari_ Hessiano (02/05/14)
Sintesi_Serie_Numeriche (02/05/14)
Equazioni_Differenziali (02/05/14)
Sintesi_Integrali(02/05/14)
Sintesi teoria integrali definiti e indefiniti(02/05/14)
Integrazione argomenti programma (6/05/14)

LE DERIVATE PARZIALI
Per studiare le derivate parziali partiremo, come nel caso delle derivate ordinarie, dal rapporto incrementale, o meglio dai rapporti incrementali essendo la funzione Z=f(x,y).
Infatti, data una funzione f(x; y) si definisce rapporto incrementale parziale di f rispetto a x relativo al punto P(x₀; y₀) il rapporto fra l'incremento parziale ∆xf e l'incremento ∆x della variabile x:
Allo stesso modo, definiamo il rapporto incrementale parziale di f(x,y) rispetto a y relativo sempre al punto P(x₀; y₀) come il rapporto tra l'incremento parziale ∆yf e l'incremento ∆y della variabile y:
Stabilito ciò, possiamo andare a definire le derivate parziali.
Si chiama derivata parziale della funzione f(x; y) nel punto P(x₀; y₀) rispetto alla variabile y il limite, se esiste ed è finito, del rapporto incrementale parziale rispetto a y al tendere a 0 dell'incremento ∆y:
Altri modi per indicare la derivata parziale della funzione f(x; y) rispetto a x sono:
* f'x(x₀; y₀);
* Dfx(x₀; y₀).
Analogamente, ulteriori modalità per indicare la derivata parziale di f(x; y) rispetto a y sono:
* f'y(x₀; y₀);
* Dfy(x₀; y₀).
* Dfy(x₀; y₀).
Dopo tutte queste definizioni formali, procediamo con il calcolo delle derivate parziali. Per derivare una funzione di 2 variabili reali rispetto a una variabile basta derivare rispetto al parametro selezionato e considerare l'altro come una costante. Il tutto diverrà molto più chiaro dopo aver osservato alcuni esempi. Prendiamo la funzione f(x; y) = x² + 3y. La sua derivata parziale rispetto a x sarà:
.jpg)
La sua derivata parziale rispetto a y sarà invece:
.jpg)
Prendiamo un'altra funzione: f(x; y) = 3x²y + 5x² - 2y².
La sua derivata parziale rispetto a x sarà:
La sua derivata parziale rispetto a y sarà:
Potremmo adesso calcolare le derivate seconde. Come si fa? Innanzitutto prendiamo la derivata parziale di tale funzione rispetto a x, che abbiamo detto essere 6xy + 10x.
La derivazione può seguire 2 strade: o deriviamo nuovamente rispetto ad x, oppure deriviamo rispetto a y. Eccole entrambe:
.jpg)
L'analogo vale per quanto concerne la derivazione rispetto alla y.Riprendiamo allora il risultato della prima derivazione rispetto alla y, ovvero 3x² - 4y e compiamo il medesimo procedimento:
.jpg)
.jpg)
Possiamo verificare che le 2 derivate miste sono uguali a (6x). Ebbene, per il teorema di Schwarz, possiamo asserire che risultano uguali le derivate miste delle funzioni elementari e di tutte le funzioni che si ottengono componendo le stesse tramite operazioni algebriche.
 |
| Z=f(X,Y) |


A)DEFINIZIONE DI FUNZIONE DI DUE VARIABILI
Se consideriamo una coppia di numeri reali X,Y e ad essi facciamo corrispondere un altro numero reale Z, allora abbiamo determinato una funzione reale di due variabili reali.
In generale si dirà FUNZIONE REALE DI DUE VARIABILI REALI una relazione che associa ad ogni coppia ordinata di numeri reali (X,Y), appartenenti ad R^2,uno ed un solo numero reale Z .
Tecnicamente si scriverà: (X,Y) --> Z = f(X,Y).
Si definirà invece FUNZIONE REALE DI N VARIABILI REALI una relazione che associa ad ogni n-upla di numeri reali(x1,x2..xn),appartenenti ad R^n, uno ed un solo numero reale Z.
Tecnicamente si scriverà: (x1,x2..xn) ---> Z=f(x1,x2...xn)
B)DOMINIO e CODOMINIO DI UNA FUNZIONE A DUE VARIABILI
Come per le funzioni ad una sola variabile si definisce DOMINIO DI UNA FUNZIONE A due VARIABILI l'insieme dei valori che possono essere attribuiti alle variabili indipendenti (X,Y) della funzione data. Si definisce invece CODOMINIO DI UNA FUNZIONE A DUE VARIABILI l'insieme dei valori che corrispondono alla variabile dipendente Z. Si tengano sempre presenti le seguenti differenze tra le FUNZIONI AD una sola VARIABILE e quelle a due VARIABILI:
1)Il GRAFICO di una FUNZIONE AD UNA VARIABILE risulta una curva rappresentabile nel piano cartesiano.
2)Il GRAFICO di una FUNZIONE A DUE VARIABILI risulta una superficie rappresentabile nello spazio a 3 dimensioni.
3)Il DOMINIO di una FUNZIONE ad 1 VARIABILE risulta l'asse reale o parte di esso
4)Il DOMINIO di una FUNZIONE A 2 VARIABILI risulta il piano R^2 o parte di esso.
In base al 4) caso si può allora dire che:
a)Il DOMINIO di una FUNZIONE A 2 VARIABILI razionale non fratta risulta il piano R^2
b)Il DOMINIO di una FUNZIONE A 2 VARIABILI razionale fratta risulta il piano R^2 privato dei punti della curva presente nel suo denominatore.






.jpg)
.jpg)
.jpg)
.jpg)
.jpg)

